Multiple Testing Under Dependence
Observations from large-scale multiple testing problems often exhibit dependence in the sense that whether the null hypothesis of one test is true or not (termed underlying true state) depends on the underlying true states of other tests. For instance, in genome-wide association studies, researchers collect hundreds of thousands of highly correlated genetic markers (single-nucleotide polymorphisms, or SNPs) with the purpose of identifying the subset of markers associated with a heritable disease or trait. In functional magnetic resonance imaging studies of the brain, thousands of spatially correlated voxels are collected while subjects are performing certain tasks, with the purpose of detecting the relevant voxels. The most popular family of large-scale multiple testing procedures is the false discovery rate analysis. However, all these classical multiple testing procedures ignore the correlation structure among the individual factors, and the question is whether we can reduce the false non-discovery rate by leveraging the dependence, while still controlling the false discovery rate in multiple testing.
Graphical models provide an elegant way of representing dependence. With recent advances in graphical models, especially more efficient algorithms for inference and parameter estimation, it is feasible to use these models to leverage the dependence between individual tests in multiple testing problems. More specifically, we can use graphical models to explicitly model the underlying true states of the hypotheses as random variables to encode the dependence, and then model the observed test statistics independently given their underlying true states. We propose a multiple testing procedure based on a Markov-random-field-coupled mixture model which allows arbitrary dependence structures. In our model, the underlying true states of the hypotheses form a Markov random field, and the observed test statistics are assumed to be independent given the underlying true states.
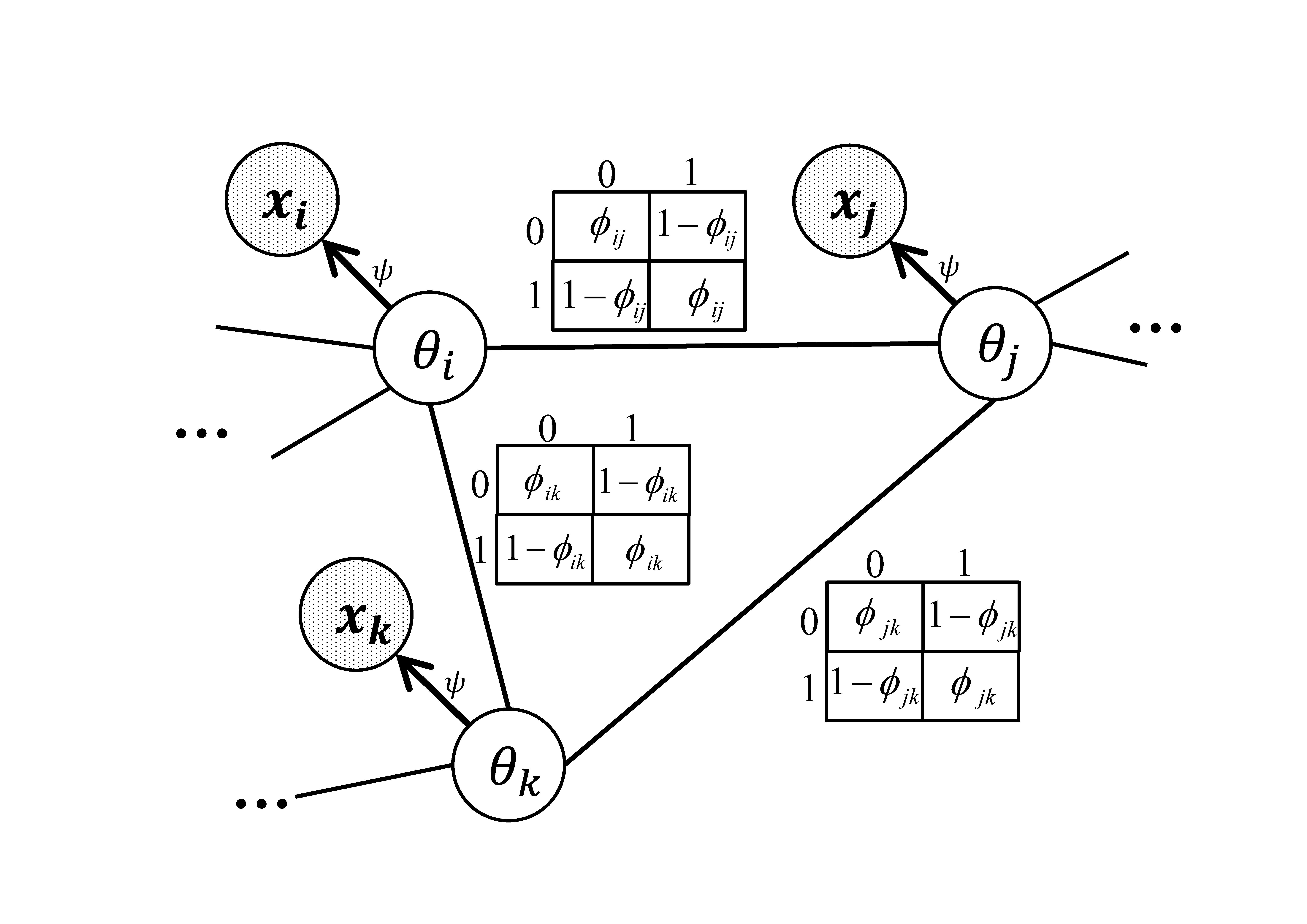
This model requires more sophisticated algorithms for parameter estimation and inference. For parameter estimation, we design a novel EM algorithm with MCMC in the E-step and a contrastive divergence style algorithm in the M-step. We show that there is a lower bound of the log likelihood which nondecreases over the EM iterations except for some MCMC error introduced in the E-step. We use the MCMC algorithm to infer the posterior probability that each hypothesis is null (termed local index of significance or LIS). Finally, the false discovery rate can be controlled by thresholding the LIS.
In addition, we design a semiparametric variation of the graphical model which nonparametrically estimates the $f_1$ function — the density function of the test statistic under the alternative hypothesis. This is particularly important in some practical problems where $f_1$ is heterogeneous among multiple hypotheses, and cannot be estimated with a simple parametric distribution. The remainder of the graphical model is still estimated parametrically. The inference of the posterior probability and the false discovery rate control in this semiparametric variation remain the same as the parametric procedure. More important, this semiparametric approach exactly generalizes the local FDR procedure (Efron et al., 2001) and connects with the BH procedure (Benjamini and Hochberg, 1995).